WHAT IS
MATH AND POLITICS TRIVIA
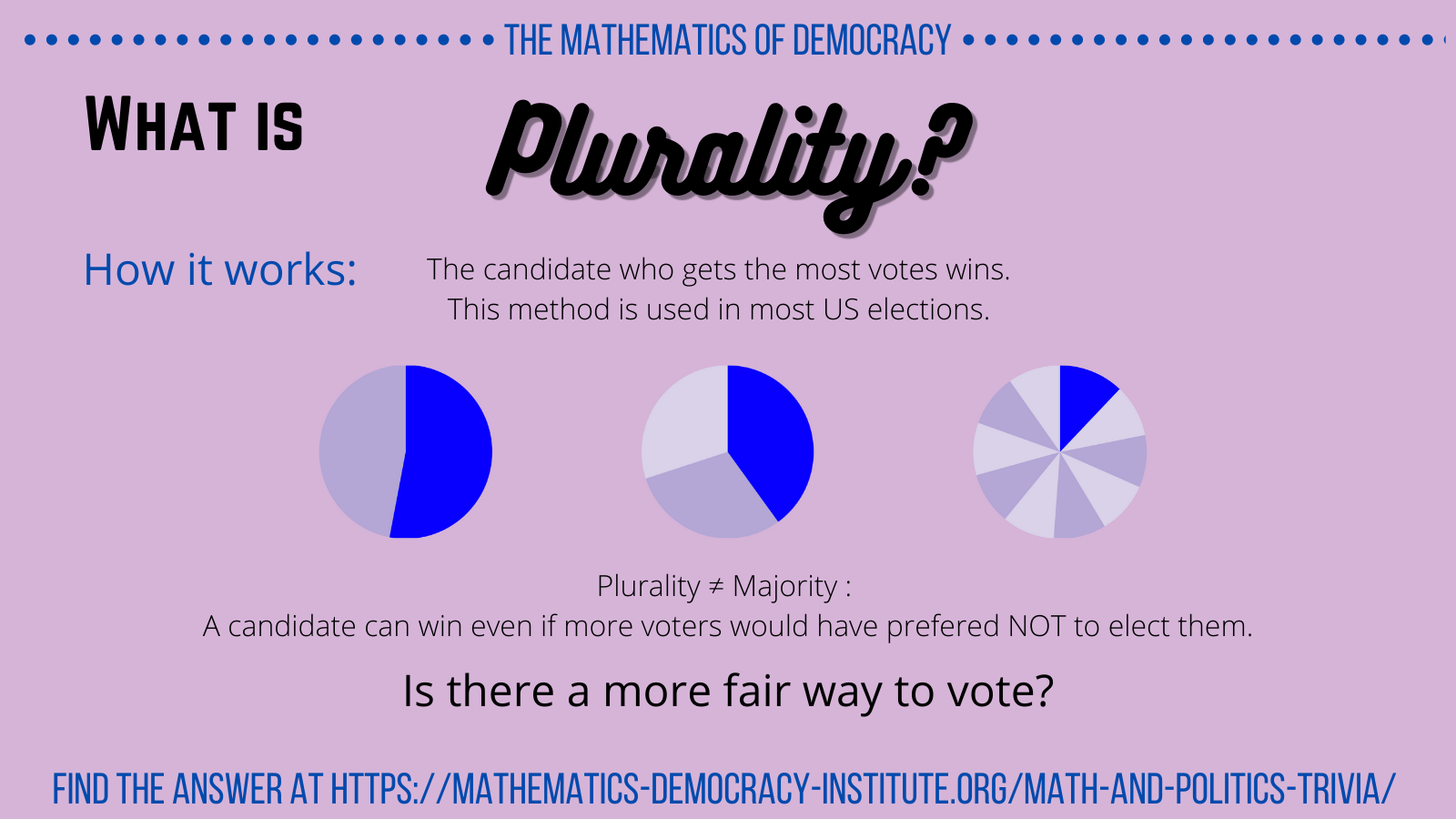
Though it is used in most U.S. elections, plurality voting has many negative consequences:
- Plurality allows a candidate who does not have to have the majority of votes to win, so they can be elected even if more voters would have preferred NOT to elect them.
- Plurality encouraged dishonest voting as voters are incentivized not to pick their true favorite candidate, skewing the perceived preferences of voters:
- If you don’t think candidate A can win, you might vote for the more popular candidate B instead, even if you really prefer candidate A.
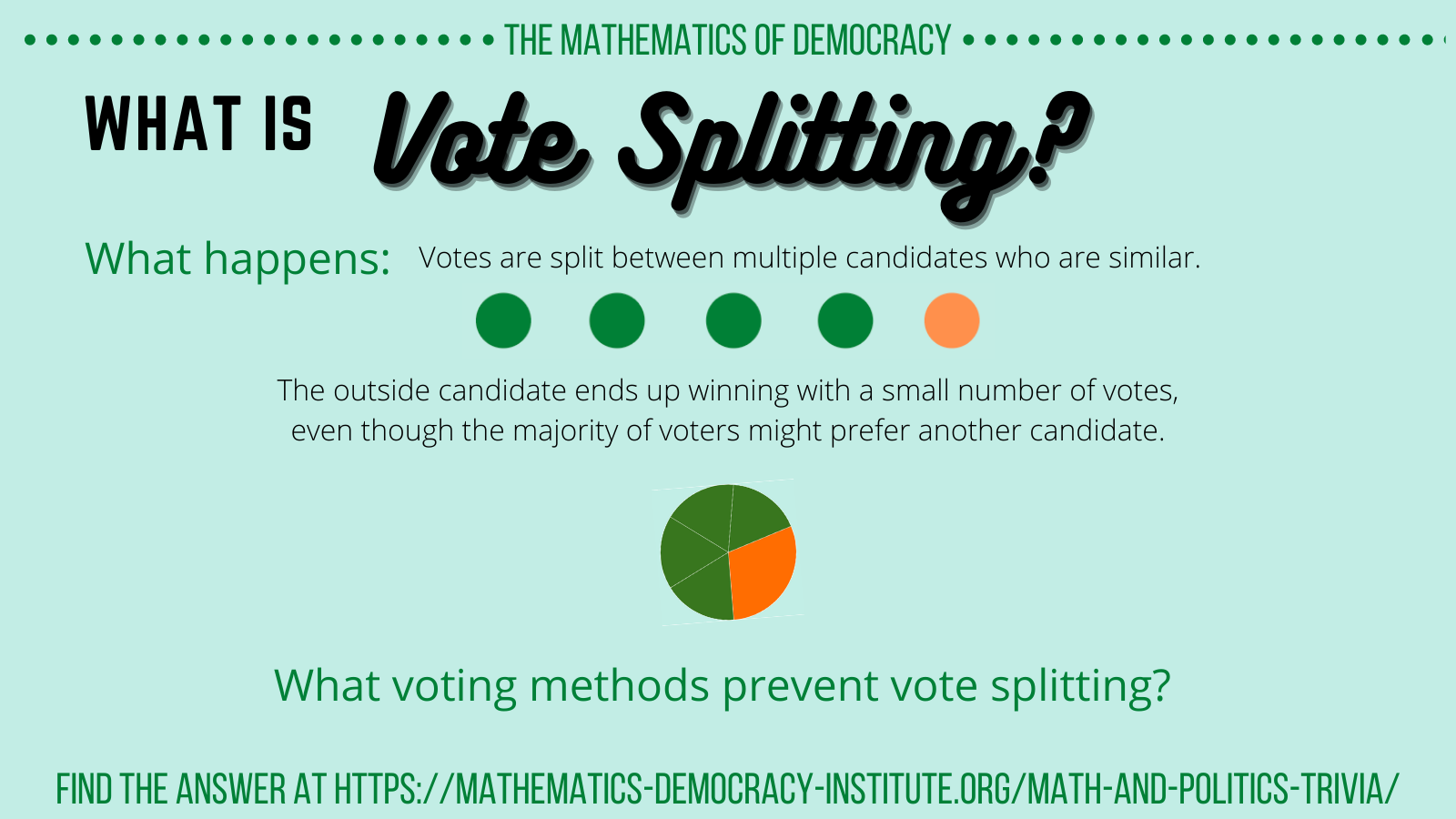
- Plurality is prone to vote splitting, so a fringe candidate has a higher chance of winning:
- For example, there might be 10 candidates who are all reasonable choices, but because they are so similar, they each win 9% of the vote, allowing another candidate to win with only 10% of the vote.
- Plurality is susceptible to the spoiler effect, where a candidate who has no chance of winning can flip an election:
- If votes are split fairly evenly between two candidates, a minor candidate can pull enough votes away from one of them to decide the election in favor of the other.
Plurality is simply not expressive enough. It is mathematically unsound. Though there is still debate about which voting method is the best, the more information voters can give about their preferences about all candidates, the better. Some possible alternatives to plurality that are more mathematically “fair” are ranked choice voting, range voting, and approval voting, among others.
Ranked Choice Voting is a better system than plurality because it is more expressive: instead of asking voters for only their first choice, voters get to rank all the candidates. The process of tallying the votes, called instant runoff, produces the best consensus candidate, reflecting the nuances of the electorate’s preferences. In particular:
- Unless there is a tie, the winner will receive the majority of votes.
- In contrast to the current plurality system where a candidate only needs the most votes to win, a candidate wins under RCV only if they have the majority of votes after some number of rounds of instant runoff.
- Voters do not have to worry about “wasting” their vote.
- There is no anxiety about wasting a vote on a candidate who is clearly not going to win, since a voter’s second place vote will still be counted if their favorite candidate is eliminated.
- Ranked choice voting avoids the spoiler effect.
- The spoiler effect occurs when a minor candidate pulls some votes away from a major candidate, causing another major candidate to win. With RCV, a vote for a minor candidate will transfer to the major candidate if the minor candidate is eliminated.
- Ranked Choice Voting encourages more diverse candidates to run.
- Since candidates can run without worrying that they will split the votes between similar candidates or act as spoilers, more people are compelled to join the race.
- Ranked choice voting discourages negative campaigning.
- Being ranked second, third, etc. matters, so candidates are compelled to appeal to a broader audience and are less likely to launch negative campaigns.
Ranked choice voting is currently used statewide in Maine, in various counties and cities, many organizations and companies, and in a number of countries around the world. In 2020, RCV is on the ballot in Massachusetts and Alaska.
Approval voting is used by the American Mathematical Society, Mathematical Association of America, American Statistical Association, and Society for Industrial and Applied Mathematics. There must be something to this method when so many mathematicians are using it! Approval voting is also used in various organizations and political parties. Voters in Fargo, MN and St. Louis, MO also recently chose to use approval voting in certain elections.
Approval voting has many advantages:
- It is not susceptible to strategic voting.
- Since voters can choose to mark multiple candidates, they can vote for their true favorite candidate and also a candidate who is more likely to win without fear of wasting their vote.
- It eliminates the spoiler effect and reduces the possibility of vote splitting.
- This encourages participation by smaller parties and outside candidates.
- It does not fall under the Arrow Impossibility Theorem.
- This theorem says that no ranked choice voting method is perfect. But approval voting is not a ranked choice method (it is a cardinal method) and Arrow’s Theorem therefore does not apply to it.
- It is easy to understand and implement on a large scale.
The simplicity of approval voting is also its downside. For many voters, approval voting is not expressive enough; if a voter checks multiple candidates, it is impossible for them to communicate which candidate they prefer the most.
Vote splitting can occur when the voting method that is used is not expressive enough. This is the case with plurality voting, the method most commonly used in U.S. elections, where people vote for one candidate and the person with the most votes wins. To illustrate, suppose there are ten similar candidates who each win 9% of the votes and one outside candidate who wins 10% of the vote. The outside candidate wins even though, if given the option, 90% of the candidate might have consolidated their votes around one of the other ten candidates.
Vote splitting occurs frequently in American elections, particularly when there are many similar candidates vying for one spot, such as during primary elections. For example, the 2016 Republican primaries had many candidates, and Donald Trump was considered the fringe candidate. However, though Trump won the plurality (but not the majority) of votes and became the Republican nominee, polling suggests that he would have lost in one-on-one elections with Cruz and Rubio.
Another high profile case of vote splitting occurred in the 1998 Minnesota gubernatorial race that had three main candidates: Republican Norm Coleman, Democrat Skip Humphrey, and Jesse “The Body” Ventura. Ventura won with 37% of the votes, compared to Coleman’s 34% and Humphrey’s 28%. Yet almost everyone who voted for Humphrey had Coleman as a second choice. This means that, though Ventura won, 62% of people actually preferred Coleman!
Voting methods that allow voters to express an opinion about every candidate are less susceptible to vote splitting. Ordinal methods like ranked choice voting and cardinal methods like approval voting and range voting are some of the solutions to this problem.
To find the Condorcet winner, start by comparing every pair of candidates. In these pairwise elections, a candidate does not have to be ranked first to win. They just have to be ranked higher than the candidate they are being compared to on the majority of ballots:
- First compare candidates A and B:
- A is ranked over B twice, so A wins.
- Then compare candidates A and C:
- C wins 2-1 over A.
- Finally, compare candidates B and C:
- B wins with two out of three of the votes.
Since each pairwise election produced a different outcome, there is no Condorcet winner in this election. This outcome can be represented by a triangle with vertices A, B, and C, and arrows pointing towards the winner in each pairwise election. These are called directed graphs. If all arrows emanate from one candidate, that candidate wins. In this instance however, there is one arrow emanating from each candidate and one arrow pointing to each candidate, so there is no Condorcet winner. This is an example of a Condorcet cycle.
The outcome of this example represents one of the main drawbacks of the Condorcet method: it does not always produce a winner. Though this voting method produces a good compromise candidate who is preferred over all of the other candidates in pairwise comparisons, the likelihood of a tie is very high since it is possible that no candidate beats all the others. Additionally, the Condorcet method fails to provide an incentive for candidates to be innovative or take a stand on controversial issues because this method can produce a winner who is simply the least offensive candidate. Several organizations and foundations use the Condorcet method, including the Pirate Party of Sweden.
To calculate the winner, we must tally the point totals. Since there are 3 candidates, a candidate gets 2 points for each first place vote, 1 point for each second place vote, and no points if they are placed third.
- A’s points = 2×3 + 1×0 = 6
- B’s points = 2×2 + 1×3 = 7
- C’s points = 2×0 + 1×2 = 2
Therefore, B wins this election.
An interesting observation is that A was actually preferred over B by 60% of the voters. In fact, A got the majority of first-place votes, yet B was elected the winner. This is an example of how Borda Count fails the Majority Criterion. A voting method satisfies the Majority Criterion if it always elects the candidate who receives the majority of the votes, if there is such a candidate. Even if Borda Count fails to satisfy this criterion, it tends to elect a good “compromise” candidate.
Borda Count elections are susceptible to dishonest voting, which occurs when voters do not express their real preferences on the ballots. This often results from voters believing they would be “wasting” their vote if their true preference is not widely popular. With Borda Count, since candidates get more points the higher they are placed on the ballot, the winner can be directly impacted by a voter choosing to place their real preference lower on the ballot.
Borda Count and its variants are used in elections in Slovenia, Kiribati, and Nauru. It is also used to elect winners for various awards such as the Heisman Trophy and the Eurovision Song Contest, and is implemented in a number of organizations and universities to select officials and representatives to governing bodies.
As opposed to ordinal voting methods where candidates are arranged in order of preference, range voting is a cardinal method where candidates are rated independently of each other. This means that voters can express an opinion about each candidate without having to compare them to the other candidates, avoiding many of the mathematical complications or ordinal voting methods. For example, the 2000 American Presidential election is widely believed to have been affected by the spoiler effect: third party candidate Ralph Nader was politically similar to Al Gore, so he likely pulled votes from Gore, causing George Bush to win. Yet, most Nader supporters would have (probably) voted for Gore over Bush, in which case Gore would have won. If range voting had been used instead, voters for Nader could have expressed a high preference for both Nader and Gore, avoiding a spoiler.
Range voting also discourages dishonest voting, since all voters may express an opinion about every candidate, including their true preference and those they believe are more likely to win. Additionally, range voting has the advantage of being both intuitive while also expressive. Compared to approval voting, another common cardinal voting method, range voting is more sensitive to voter preferences. The larger the numerical range, the more expressive voters can be. This method is also simple enough for voters to understand, and the technology to employ it already exists.
If a voter does not have enough information about a candidate, range voting allows them to avoid expressing any opinion about them. The winner of the election is calculated by adding up the total score for each candidate and then dividing that number by the amount of voters who gave them a score, so no candidate is penalized by not having a broad coverage. To avoid an unfair advantage to voters with a small but enthusiastic fanbase, a set number of “fake” votes of a set score can be given to every candidate so that the winner is calculated by dividing both the real and fake votes by the number of voters (including fake voters) so that the effect of a small but enthusiastic voting block is minimized in favor of a more broadly popular candidate. This is fair since every candidate receives the same number of fake votes.
Range voting is used in many Olympic sports and some TV competitions like The Voice.
This example was taken from The Mathematics of Elections and Voting by W. H. Wallis. There are 110 total votes cast in this election. Since no candidate got over 110/2 = 55 first-place votes, there is no majority winner. Since A got the most first-place votes, A is the plurality winner.
Now let’s look at the instant runoff winner: E has the least first-place votes, so E is removed, and the retabulation looks like:

Now D has the least first-place votes, so we get:
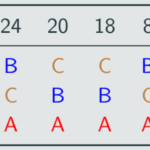
Finally, B is removed:

Since C ends with the most votes, C wins the instant runoff.
We could have also performed a simple runoff instead of instant runoff. Here, we only consider the two candidates with the most first-place votes and eliminate the rest. Therefore, we just look at A and B:
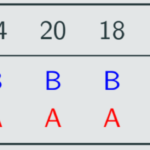
B wins the runoff with 74 out of 110 votes.
Using Borda Count, we give each candidate 4 points for every first-place vote, 3 points for every second-place vote, etc., and zero points for last place. The point totals are:

D wins the Borda Count.
For the Condorcet method, we try to find a candidate who wins against every opponent in a pairwise contest. We find that E wins over:
- A by a vote of 74-36
- B by a vote of 66-44
- C by a vote of 72-38
- D by a vote of 56-54
So E is the Condorcet winner.
This means we have:
- No majority winner.
- A is the plurality winner.
- B is the runoff winner.
- C is the instant runoff winner.
- D is the Borda count winner.
- E is the Condorcet winner.
Thus, for one profile, there are five possible winners depending on what method is used to tally the votes! This shows how difficult it is to extract group preferences from individual opinions. This is the basis for the subject of social choice theory, a field at the intersection of mathematics, political science, history, economics, psychology, and other fields. The voting method matters, so stay tuned for future trivia about how we might decide which method is best based on some desirable properties.
Cumulative voting is a very expressive cardinal voting method. One main advantage is increased minority representation: voting minorities can concentrate large portions of their vote on a candidate they prefer. Since many other voters choose to split their vote into smaller fractions across many candidates, a minority candidate with strong support has a better chance of winning. Additionally, cumulative voting is easily modified for multi-winner elections, where voters are given the same number of votes as there are seats to elect. Then they may allocate these votes however they choose. Yet, cumulative voting has several pitfalls.
First, it may be too expressive. Since each voter can split up their vote among the candidates however they please, there is significant freedom for each voter. This increases the complexity of the method, leading to a high risk of user error. Each voter’s fractional votes must add up to one, creating the chance of invalid votes if a voter miscalculates. Due to this complexity, elections that use cumulative voting often see low voter turnout.
Next, this method is susceptible to strategic voting because assigning part of a vote to one candidate is taking away a potential vote from another. Therefore, if a voter actually prefers a fringe candidate with a low likelihood of winning, they may see it as unwise to waste all or part of their vote on that candidate. Instead, they are incentivized to give a larger portion of their vote to a candidate who is seen as more likely to win, so their ballot may not express their honest opinions.
Cumulative voting has a history of use in England and Illinois in the nineteenth century. Now, it is used in district elections in several counties across the United States, often in response to past lawsuits about inequitable voting practices. Many corporations use cumulative voting, giving each voter the same number of votes as their shares in the company.
These four criteria may seem like the bare minimum for what we expect from a voting system, but they cannot be taken for granted. For example, a dictatorship (one voter decides the election outcome) fails the anonymity criterion because if the dictator switches ballots with someone who voted differently, the outcome of the election changes. An example of the failure of neutrality is a monarchy (one candidate is automatically the winner, regardless of voter preference).
May’s Theorem says that if a voting method for a two-candidate election is anonymous, neutral, and monotone, then it is a quota method. A quota method is the procedure whereby a number is set such that any candidate who reaches or surpasses that number of votes wins. We can see that quota methods satisfy these three criteria:
- Anonymity is satisfied, because it doesn’t matter which voters fulfil the quota of votes for a candidate to win. Therefore, all voters are treated equally.
- Neutrality is satisfied because both candidates are held to the same quota, so they are also treated equally.
- Monotonicity is satisfied, because a candidate who has already received the quota of votes still wins if they surpass the quota.
A consequence of May’s Theorem is that the only voting method for an election with two candidates that is anonymous, neutral, monotone, and nearly decisive is the simple majority method, namely one where the quota is set exactly at half the number of voters. To see this, we already know from May’s Theorem that a method that satisfies the first three criteria must be a quota method. Now what’s left is to explore how decisiveness relates to what quota is chosen. If the quota is less than half the number of voters, then both candidates could reach it and “win,” producing a tie. Similarly, if the quota is set at more than half the number of voters, it would be possible that no candidate reaches it, which is another kind of a tie. Therefore, neither of these options are nearly decisive. But if the quota is exactly half the number of voters, a candidate needs the majority of votes to win, and the election will always produce one winner unless the candidates get the exact same number of votes. May’s Theorem essentially says that, if there are two candidates, the simple majority method is the best possible voting system.
The Gibbard-Satterthwaite Theorem states that in a ranked-choice election with more than two candidates, the only voting method that is not susceptible to strategic voting is dictatorship. Although the concept of strategic voting was first observed in the late nineteenth century, this theorem was proved independently by Allan Gibbard and Mark Satterthwaite in the 1970s. The Gibbard-Satterthwaite Theorem is a consequence of Arrow’s Impossibility Theorem. One can show that any voting method that is non-manipulable and non-dictatorial must also satisfy the Pareto criterion and Independence of Irrelevant Alternatives. However, from Arrow’s Impossibility Theorem we know this is not possible in ranked elections with three or more candidates. In a dictatorship, one voter, the dictator, decides the election. This dictator will only get their preference by voting honestly, and other voters do not have a say in the election, so they have no incentive to lie about their preferences. Therefore, dictatorship is the only voting system that is non-manipulatable in ranked elections with more than three candidates. Like Arrow’s theorem, this statement implies not only that no existing non-dictatorial and non-manipulatable voting methods satisfy these conditions, but also that a voting method satisfying these properties cannot exist.
This means that in elections where ranked choice or plurality is used, a voter’s sincere ballot may not always best advance their preferences. They may thus be incentivised to vote strategically. In the US, this can be seen most often in primary elections, where voters may choose a more popular candidate than “waste” their votes on their true preference who is unlikely to win.
A voting system should empower voters to share their honest opinions about the candidates. On the other hand, we clearly do not want to use dictatorship as our election method. The Gibbard-Satterthwaite and Arrow’s Impossibility Theorems thus suggests that we should be mindful of the fact that no non-dictatorial ranked choice voting system is perfect. It’s important to note that neither theorem gives insight into how often or when an election will fail the Pareto criterion or the IIA, or be manipulable by dishonest voting. Similarly, these theorems do not apply to cardinal voting methods, where candidates are not ranked against one another.
Remember that cumulative voting is a cardinal voting method where voters submit a fractional ballot, splitting their one vote between candidates however they want. In contrast, using discrete cumulative voting, voters get the same number of votes as there are candidates to elect. Typically, voters cannot split their votes further into fractions, but they can spread them among the candidates however they wish. If there are n candidates, this amounts to giving each voter one full vote that they may split into n equal parts. This change imposes a constraint on expressiveness: using cumulative voting, voters can split their vote using any denominator they choose. Whether they choose to give a candidate 1/10 or 1/11 for example, is completely up to their discretion. In contrast, discrete cumulative voters must use n as their denominator. For instance, if there are 11 candidates, voters can only reward candidates with 1/11, 2/11, 3/11 etc of their total vote.
Discrete cumulative voting is susceptible to the same problems as cumulative voting. First, election results can be manipulated through strategic voting. While voters can spread their votes among all the candidates they support, voters may not be incentivized to vote honestly if their favorite candidate is unlikely to win. Instead of “wasting” votes on their favorite candidates, they may opt to place more or all of their votes on more popular candidates. Therefore, despite the high level of freedom in discrete cumulative voting, this method does not always incentivize voters to share their true preferences.
Additionally, this freedom may be a downside of discrete cumulative voting. With n total votes, voters have many decisions to make. They must not only decide which candidates to support but also how many votes to allocate towards them. These tactical decisions may feel overwhelming to some voters.
Discrete cumulative voting is most popular with corporations electing people to positions such as trustees or board directors, because it provides a convenient way to select multiple candidates while giving voters a lot of freedom with their votes. Many argue that, in contrast to a plurality election where the top n candidates are chosen, discrete cumulative voting helps support fringe candidates. Even though voters may not vote honestly, with n total votes, they may feel like they can give at least some of their votes to a candidate who they like but who is less likely to win.
The American 2000 presidential election is the most famous example of the spoiler effect. The main candidates were Republican George W. Bush and Democrat Al Gore. Additionally, there was a third party candidate, Ralph Nader (Green party). The election was so close it came down to Florida’s 25 electoral votes. The tally was:
| Candidate: | Popular Vote: |
| George W. Bush | 2,912,790 |
| Al Gore | 2,912,253 |
| Ralph Nader | 97,488 |
| Others | 40,579 |
Bush won the state by only 537 votes! Though Gore won the national popular vote by 547,398 votes, Bush won the election. Yet most Nader supporters would have (probably) voted for Gore, in which case Gore would have won. It is important to note that we do not know for certain what would have happened if spoiler candidates were not running because we do not know how people who voted for them would have voted otherwise. We can only make educated guesses based on polls, which can be unreliable. For example, the 1992 presidential election between George H. W. Bush (Republican), Bill Clinton (Democrat), and Ross Perot (Independent) is still debated. In fact, up to 7, or about about 12%, of presidential elections in the U.S. history might have been decided by the spoiler effect:
- Trump-Clinton (2016)
- Bush-Gore (2000)
- Clinton-Bush (1992)
- Wilson-Roosevelt (1912)
- Harrison-Cleveland (1888)
- Taylor-Lewis (1848)
- Polk-Clay (1844)
Is this a lot? Is it acceptable? The answer is subjective, but we can all agree it would be better to choose a voting method that is less susceptible to spoiler effect. Plurality is extremely susceptible, while ranked-choice voting is less so. Cardinal methods like approval voting effectively eliminate it, because they allow voters to indicate their preference for multiple candidates, major and minor.
There are 32 voters, so the quota is the floor (closest integer lower than the number) of
32/(3+1) + 1 = 8+1 = 9
Notice that by defining the quota in this way, there cannot be more than N candidates achieving the quota: if 4 candidates achieved this quota, there would need to be at least 4×9 = 36 votes, but there are only 32 voters.
Now we look at the voting profile:
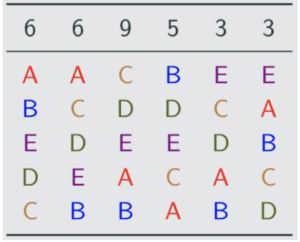
A has cleared the quota with 12 first-place votes, so they are elected. A has a surplus of 3 votes. Those votes are to be distributed to the second choices of those voters who had A in the first place. The distribution has to happen in proportion 6 : 6 according to the first two columns. So B and C get 1.5 votes each in the first two columns.
New profile has A removed and extra votes awarded to B and C:

C also cleared the quota with 10.5 first-place votes, so they are elected. C has a surplus of 1.5 votes. Those votes are to be distributed to the second choices of those voters who had C in the first place, which is D for all those voters. D gets 1.5 votes in proportion 1.5 : 9 according to the first two columns. So D gets 1.5/10.5 · 1.5 = 0.2 votes in first column and 9/10.5 · 1.5 = 1.3 in the second column.
New profile has C removed and extra votes awarded to D:
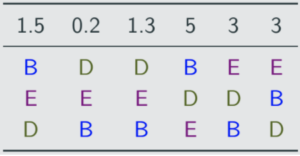
Nobody meets the quota. D has the least first-place votes, so eliminate them and shift the table as in instant runoff:
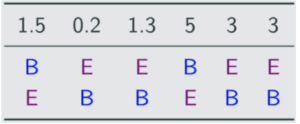
Now E has 7.5 votes and B has 6.5 votes, so E is the third person elected.
Since single transferable vote generalizes instant runoff, it retains the pros and cons of instant runoff: it avoids the spoiler effect and encourages more diverse candidates, but it is still impacted by Arrow’s Impossibility Theorem.
First we will find the Instant Runoff Voting (IRV) winner. Since there is no candidate who wins the majority of the votes, we eliminate the candidate with the least first-place votes, in this case B. Then we shift all the votes to reflect B’s elimination:
| # of voters: | 35 | 33 | 22 | 10 |
| A | C | C | A | |
| C | A | A | C |
Now we tabulate the results again. Here C wins the majority of the votes, so C wins the election. However, B is the Condorcet winner: comparing candidates A to B, 65% percent of voters prefer B. Similarly, 67% of voters would choose B over C. If B has the broadest appeal, why wasn’t she elected under IRV? The first step in IRV is to eliminate the candidate with the least first place votes. Centrist candidates tend not to have many first place votes (voters often prefer the candidate who is more ideologically similar to them), but appear many times as a second choice (voters from all parties would be okay with them being elected). Therefore, IRV puts these candidates at a disadvantage as their risk of being eliminated early in the calculation is high. It is important to note that this effect corresponds to the ideological center candidate, relative to the other candidates in the race.
IRV is not the only voting method that is susceptible to the center-squeeze effect: we often see it occur in plurality elections where voters never even get a chance to express their second choice. This shows that many elections may promote more ideologically extreme candidates and are susceptible to strategic voting, where voting dishonestly is incentivized. Voting methods such as approval voting and the Condorcet method are immune to the center-squeeze effect.
If every voter voted for their honest first choice, then the moderate votes would likely be split between the moderate candidates and so the radical candidate is likely to win. Duverger’s law says that, anticipating this, the moderate voters would choose the moderate candidate who is most likely to win, prioritising a moderate candidate getting elected over a radical one instead of voting for their favorite moderate candidate. Therefore, smaller parties are not likely to join in plurality elections because they know voters won’t see them as “likely to win” so they are unlikely to receive many votes.
Duverger’s Law is also based on the premise that in single-candidate plurality elections, the threshold to elect one candidate is relatively high. In plurality elections, a candidate wins if they get the majority of the votes. The fewer there are candidates for voters to choose from, the higher the winning percentage of votes is. Therefore, smaller political parties are unlikely to arise in these environments because the chances of them being able to get anyone elected to office are so low, even if they have a decent amount of support.
Therefore, political systems that use plurality often feature two prominent parties. Druverger’s law has been used to explain why the United States consistently has a two-party system, even though the two political parties have changed over time. As a corollary, Druverger’s law states that two-party systems are less likely to arise in countries that use proportional representation, such as instant runoff voting.
Though Duverger’s law states that plurality elections make two-party systems more likely, it does not guarantee that multi-party systems cannot arise in these conditions. For example, the Philippines, Canada, India, and the United Kingdom all use plurality for national elections and also regularly have candidates from three or more parties in their parliaments/House of Commons. Due to the existence of these counterexamples, some scholars have voiced doubts about the validity of Duverger’s Law.
Though they sound similar, the Pareto and Unanimity criteria are distinct requirements! For example, take an election where candidate A is ranked above candidate B on every ballot. If the election satisfies the Pareto condition, candidate B cannot be the winner (because they are always ranked below candidate A). However, this does not guarantee candidate A is the winner: if candidates A and B were the bottom two on every voter’s ballot, then candidate A would not win. Thus, the Pareto condition is really a requirement about which candidates cannot win an election while Unanimity is about which candidate should win.
But Pareto and Unanimity are related! If an election satisfies the Pareto criterion, it is also unanimous. To see this, suppose we have a method that satisfies the Pareto condition. So we know that if every voter ranks candidate A first, then candidate A is above candidate B on every ballot, so the Pareto condition mandates that candidate B cannot win. Similarly, candidate A is above candidate C on every ballot, so candidate C cannot win. Since this is true for each of the other candidates, candidate A must win, and the unanimity criterion is satisfied.
The converse is not necessarily true: There are some voting methods that satisfy Unanimity but not the Pareto criterion. For example, Agenda is a voting method often used in sports tournaments. It starts with an ordering of the candidates. Then the candidates are compared in head to head match-ups in that order. As soon as a candidate loses in a match-up, they are out of the race. The last candidate standing wins. For example, say an agenda is given listing the candidates in the order A, B, C, D. First, A and B are compared. If A is ranked higher on more ballots than B, then B is out of the running and we next compare A and C. If B is ranked higher on more ballots than A, we then compare and D and C. The winner of this head-to-head matchup is the overall winner.
Agenda voting satisfies the Unanimity criterion; if every voter ranks candidate A above all others, then candidate A must be ranked higher than every other candidate in a head to head match-up, so candidate A will win, no matter where they appear in the initial ordering of candidates. However, Agenda voting can violate the Pareto criterion. Say there is an election with three ballots:
| Ballots: | |||
| First choice: | A | C | B |
| B | A | D | |
| D | B | C | |
| Last choice: | C | D | A |
Now say that the order of the candidates is given as A, B, C, D. First, A wins 2 to 1 over B. Next we compare A and C: C is ranked above A on two of the three ballots, so C moves on. Finally we consider C vs D and find that D comes out victorious. Observe that D is always ranked below B, yet D still wins!
In a two candidate election, Unanimity and Pareto are in fact equivalent, since the only way for all voters to rank candidate A above candidate B is for them to unanimously vote for candidate A.
In previous trivia, we discussed how a potential tie in a presidential election would be broken. For elections involving state representatives in the House and Senate, each state has their own tiebreaking procedures. The most common (used by 28 out of 50 states) is using chance! In these states, tied candidates draw lots, flip a coin, draw cards or use another randomized method to decide who won the election. The second most popular method is a redo of the whole election: in 14 states, if candidates tie, another election between the candidates who tied are conducted. In 5 other states, other state politicians, like the governor or members of the state legislature, choose the winner.
Several states have more unique tiebreaking methods. In North Carolina, if more than 5,000 votes were cast in a tied election, a new election is held between the tied candidates. If instead the election had fewer than 5,000 votes, whichever canvassing board oversaw the election gets to pick the winner. In Texas, if neither candidate drops out of the race, the candidates may choose to either rerun the election between them or cast lots and leave their fate to chance. New Jersey is the only state that has not established tie breaking procedures.
Since plurality is nearly decisive, for two candidates to tie in most American elections, they must get exactly the same number of votes. This may seem unlikely, but ties do happen, especially in smaller elections with lower turnout. For example, election officials in Nevada in 2016 and 2020 had to employ their caucus election tiebreaker: If two candidates tie, they draw cards with the highest card winning. Specifically, the cards must come from a new deck that has been shuffled at least seven times, and aces are counted as high. In 2018, David Yancy won a seat in the Virginia state legislature when his name was drawn from a bowl (made by a local artisan) containing both his and his opponent’s names. Drawing names from a hat is a common variation of this tiebreaker. Some methods are more convoluted: In a local city council race in Neptune Beach, Florida, the tied candidates’ names were put in a hat. The candidate whose name was drawn chose heads or tails for a coin toss, and whoever won the coin toss got to choose who drew a numbered ping pong ball first. Richard Arthur won by picking the higher numbered ball (12 vs 4) in the last stage.
With many legislatures, both at the state and federal levels, the difference between the number of candidates of each party is slim. Therefore, the result of a tied election can have real consequences. For example, David Yancy, who owed his seat in the Virginia House of Delegates to chance, pushed the balance of legislatures into Republican control, while a win for his opponent would have meant a 50-50 split.
To calculate the winner of this election, we see that both candidates B and C are not placed last on any ballots, so they initially tie with 100 points each. Then, to break this tie, we consider the election between just these two candidates. Now the ballots look like:
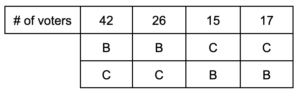
Since candidate B is placed last 32 times and candidate C is placed last 48 times, candidate B wins this election using the antiplurality method.
If instead plurality was used to calculate the winner, only the voters’ first choice votes would be considered and the ballot profile looks like:

Since A has the most first-place votes, A is the plurality winner. Note that on every other ballot that does not have A placed first, A is placed last. Candidate B, the winner of the antiplurality election, is a more moderate candidate: she isn’t as divisive as A to voters. This shows the trend of the antiplurality method to select the “least disliked candidate” as opposed to the “most liked.”
In the above example, it might make sense that candidate B should win the election over candidate A since most voters strongly disliked candidate A. However, the structure of the antiplurality method means it can fail to elect the majority winner of an election. For example, say there is an election between three candidates E, F and G, with:

In this election, candidate E is not only the majority winner, but clearly the most preferred candidate: only one voter liked any other candidate over E. Yet, according to the antiplurality method, sinceF has no last place votes at all, candidate F is the winner. This example also shows that the antiplurality winner can have no first place-votes at all! Because of these issues, antiplurality is more valuable in theory than it is used in practice.