Quantification of Power

The UN security council has five permanent members (U.S., China, England, France, and Russia) and ten that rotate (currently Estonia, India, Ireland, Kenya, Mexico, Niger, Norway, Saint Vincent and the Grenadines, Tunisia, and Vietnam). A measure passes if nine members vote for it, and the five permanent members all have veto power. To represent this system, we know that the five permanent members must have the same weight associated with their votes and the quota cannot be reached if any one of them does not vote for the measure (due to their veto power). We also know that the rotating members’ votes must have the same weight and a measure can only pass if all five of the permanent members and four rotating members vote for it. One way to write this as a weighted system is V(49; 9, 9, 9, 9, 9, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1). Equivalently, it can be represented as V(39; 7, 7, 7, 7, 7, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1). These two voting systems are “isomorphic,” since the winning combinations are the same.

While not everything can be represented as a weighted voting system (for example, the U.S. legislative system), weighted voting is useful for observing and measuring the power of a voter in an election. For instance, suppose a parliament has representatives from three parties:

• A with 49 members,
•  B with 49 members,
•  D with 2 members.

A simple majority (≥ 51 votes) wins the vote. So this is a V(51; 49, 49, 2) weighted voting system.  D looks disadvantaged, but that’s not true  – D has the same decision-making power as A and B. If any two parties decide to vote together, they win. It doesn’t not matter how the third one votes! So V(51; 49, 49, 2) and V(2; 1, 1, 1) are isomorphic. D has only 2% of the votes but has the same influence as the other parties.

A real-life example is the U.S. Senate in 2001, which had 50 Republicans and 50 Democrats. Jim Jeffords, a Republican, became an independent. The vice-president was a Republican, so the division in the Senate became 50-50-1. Neither the Republicans nor the Democrats could accomplish anything unless Jeffords joined them. Jeffords became the most powerful Senator; in fact, he had all the power! Clearly the amount of votes a voter has does not correlate to the power of their vote. There are multiple ways to quantify this influence. Stay tuned for more on the quantification of power in future trivia posts.

We can represent this as the weighted voting system V(12; 4, 4, 4, 2, 2, 1). There are 2^6 = 64 total coalitions. In general, when there are n voters, there are 2^n coalitions, the number

of subsets of a set with n elements. For large n, this is an enormous number, so the Banzhaf Power Index can be difficult to compute. 

For the European Economic Community, the winning coalitions and their critical voters are:

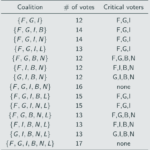
There are 42 instances when a voter is critical. France, Germany, and Italy are critical 10 times, Belgium and Netherlands 6 times, Luxembourg zero times. So 

Power index of France = 10/42 = 0.24 = 24%

Power index of Germany = 10/42 = 0.24 = 24%

Power index of Italy = 10/42 = 0.24 = 24%

Power index of Belgium = 6/42 = 0.14 = 14%

Power index of Netherlands = 6/42 = 0.14 = 14%

Power index of Luxembourg = 0/42 = 0.00 = 0%

Luxembourg is a dummy voter: it had no power even though it had a vote. It could never affect the outcome of an election. 

The Banzhaf Power Index can also be used to calculate the power of each state in the electoral college, the power of the U.S. President, the power of each member of the UN Security Council, and much more.

We see in the last column that big states seem to have slightly more power than their allocation of electoral votes. Small states benefit from the “+2” effect of adding electoral votes that correspond to the senators, because the impact of these two votes is larger when they have a smaller number of electoral votes corresponding to their representatives. The Banzhaf index suggests that this is corrected in some way if we think of states as individuals and presidential elections as a weighted vote. However, one can also ask whether about how much power the people in each state have, and this leads to a different analysis: in that case, voters in swing states are a lot more powerful since a handful of their votes can change the outcome of the election (remember the Bush-Gore election and 537 votes in Florida that decided the election). This notion of power is derived by calculating the probability of any given voter casting the decisive vote, the idea behind the Shapley-Shubik power index. Stay tuned for more on this in future trivia posts!

To find the power index for each voter, we must look at every possible sequential coalition (order matters!). Here, the sum is in blue until the quota of 16 is cleared. The last blue voter is pivotal.

A is pivotal 10 times, B is pivotal 6 times, C is pivotal 6 times, D is pivotal 2 times, and there are a total of 24 possible coalitions. This means:

Power index of A = 10/24 = 0.42 = 42%

Power index of B = 6/24 = 0.25 = 25%

Power index of C = 6/24= 0.25 = 25%

Power index of D = 2/24 = 0.08 = 8%

These calculations show that A has 50% more votes than B but has more than 50% extra power over B. Also, A has 71% more votes than C, and has about the same amount of extra power over C, and B and C have different numbers of votes, but they have the same power. 

In general, if we have n voters, then the total number of sequential coalitions = n! = n · (n − 1) · (n − 2)· · · 2 · 1. To explain, think of forming a sequential coalition as having n slots into which we want to place the voters. Then

For the first slot, we have a choice of n voters;

For the second slot, we have a choice of n − 1 remaining voters;

For the third slot, we have a choice of n − 2 remaining voters; etc.

For the last slot, we have a choice of just one remaining voter.

The total number is the product of all the choices (Multiplication Principle) which is n!. 

In contrast to the Banzhaf power index, the order in which voters join a coalition matters in the Shapley-Shubik calculations. For example, the Banzhaf Power index treats the coalitions A,B,C,D the same as D,C,B,A, whereas Shapley-Shubik treats them as distinct. This makes sense since voters often decide whether to join a coalition based on who is already in it. We will examine how Shapley-Shubik and Banzhaf power indices differ in their quantifications of power in important examples in future trivia posts.

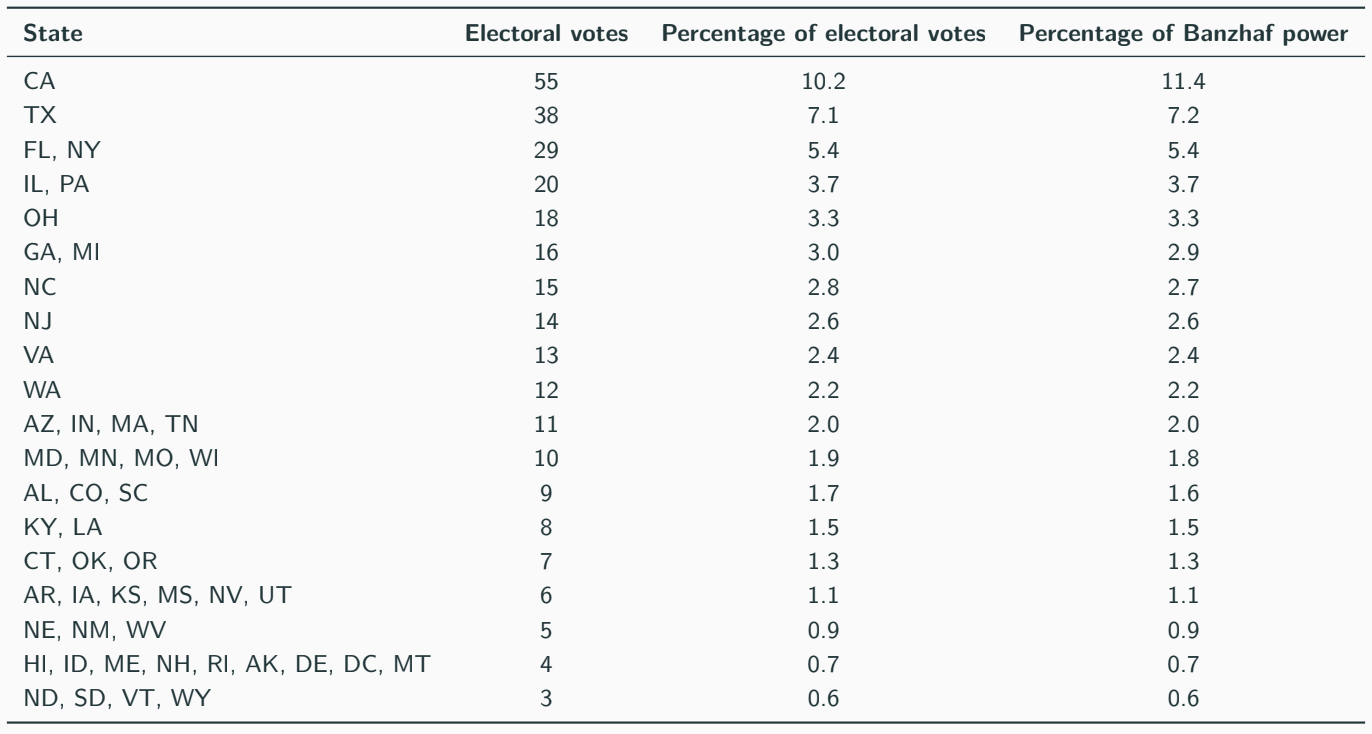
Recall from previous trivia that a voter is critical for a winning coalition if, without them, the coalition does not have enough votes to win. In this case, there are 2^51 = 2,251,799,813,685,248 possible coalitions, so the calculations are best done by computers. Here is the Banzhaf power of the states in the electoral college:

Comparing the percentage of electoral votes and Banzhaf power, it seems that big states have slightly more power than their allocation of electoral votes. A state’s electoral votes are based on the number of their Congressional representatives, so small states benefit from the “+2” effect of adding electoral votes that correspond to the senators. These calculations using the Banzhaf Index suggest that this is corrected in some way if we think of states as individuals and presidential election as a weighted vote. However, this doesn’t tell us how much power each individual voter has, which leads to a different analysis. In this case, voters in swing states are a lot more powerful since a handful of their votes can change the outcome of the election. For example, in 2000, 537 votes in Florida decided the election between Bush and Gore.

We’ll start by calculating the Shapley-Shubik power of the president. In the American federal system, a bill passes if it gets approved by either ⅔ of both the House and Senate or half of each as well as the president. This means that, for the president to be the pivotal voter, the latter case must occur: if ⅔ of both the House and the Senate vote for a bill, the president’s opinion holds no weight. Therefore, we only need to consider coalitions where less than ⅔ of at least one of the House or Senate voted for the bill. We can start to distinguish different cases in which the president’s vote is required to pass a bill: for example, the case where exactly half of the House and Senate are in favor of the bill, so 50 senators and 218 representatives are in the coalition before the president joins. There’s also the case where 51 senators and 218 representatives vote, and another where 52 senators and 218 representatives join the coalition, etc. We can keep listing until all possibilities are represented. Then we can think about how many combinations of individual senators and representatives can occur in each case using the expression which describes the number of ways to choose k out on n people:

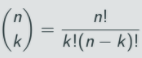
For example, in the first case mentioned above, there are 100!/50!(100-50!) ways to pick the 50 senators and 435!/218!(435-218)! ways to choose the representatives. We then get that there are 100!/50!(100-50!) x 435!/218!(435-218)! possible ways the first case can occur. These calculations for every possible case are far too large to do by hand, but computers handle them easily. Note that we need to end up dividing by the total number of sequential coalitions, or the number of ways to order 435 representatives + 100 senators + the president = 536!. The final computation finally gives 0.16047 as the Shapley Shubik index. Therefore the president has 16% of the power in the U.S. judicial system.

For the Banzhaf power index, we can also start by thinking about the circumstances in which the president is pivotal. For these calculations, it is helpful to know that an individual’s Banzhaf power is:

 (2 x the number of winning coalitions they are in) – total winning coalitions. 

Similar to the Shapley-Shubik calculations, we can calculate the total number of winning coalitions the president is in of each size (50 senators and 218 representatives are in the coalition before the president joins, 51 senators and 218 representatives, etc.) and use this formula. Note that since the Banzhaf index divides by the total number of instances in which all voters are critical, we must also complete these same calculations for each senator and representative. Using a computer, this gives us that the power of the president is 4% according to the Banzhaf index. One can also calculate that the Senate and House hold 33% and 63% of the power in the judicial system, respectively.

16% and 4% are starkly different. This is due to the elements each power index measures and prioritizes. While the Shapley-Shubik index encodes the order in which voters join a winning coalition, the Banzhaf index directly compares elected individuals in coalitions where order does not matter.

The five permanent members of the UN Security Council are the U.S., China, England, France, Russia. Currently, the other ten members are Estonia, India, Ireland, Kenya, Mexico, Niger, Norway, Saint Vincent and the Grenadines, Tunisia, and Vietnam. Since the permanent members have veto power and nine votes are needed to pass legislation, one way of representing this as a weighted voting system is V(39; 7, 7, 7, 7, 7, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1)

where the weight of each permanent member’s vote is 7, every rotating member has a vote of weight 1, and a total weight of 39 is needed to pass a piece of legislation. This representation makes sense since if five permanent members vote yes, this gives 35 votes. Then to clear the

quota of 39, four more are needed. This means 9 countries voted yes, as required. If any of permanent members does not vote yes, then the most votes that can be gathered is 4 · 7 + 10 · 1 = 38, which is not enough to clear the quota of 39. This means that permanent members have veto power.

To compute the Banzhaf index, first observe that any winning coalition must have all five permanent members in it and at least four more non-permanent members. Therefore, the winning coalitions look like:

How many coalitions is this? This depends on how many different ways we can choose 4, 5, 6, 7, 8, 9, or 10 countries out of the set of non-permanent members. The number of different ways to choose k objects out of n is

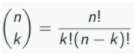
Therefore the number of ways to choose ≥ 4 members out of 10 is

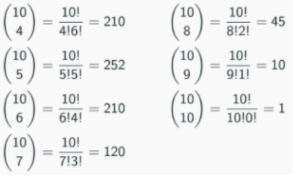
This therefore makes for 210 + 252 + 210 + 120 + 45 + 10 + 1 = 848 winning coalitions. Permanent members are critical in all of these coalitions. Non-permanent members are only critical in coalitions when there are exactly four non-permanent members, since if a non-permanent member exited such a coalition, it would no longer be winning. If there are more than four non-permanent members, any of them exiting the coalition would not matter; the coalition would still be winning. This means that non-permanent members are critical in precisely 210 coalitions. Now we want to count how many of the 210 coalitions with four non-permanent members have a particular non-permanent member, call it A. So we are looking for coalitions that contain A. But this means that these coalitions contain three more non-permanent members, and they can be any of the nine non-A countries. The number of ways of filling these three slots is the number of ways we can choose three out of nine things, i.e:

Thus each of the five permanent members is critical 848 times, and each of the ten non-permanent members is critical 84 times. So the total number of times somebody is critical is 5 · 848 + 10 · 84 = 5080. Therefore, 

 

Banzhaf index of each permanent member = 848/5080 = 0.1669 = 16.69%,

Banzhaf index of each non-permanent member = 84/5080 = 0.165 = 1.65%. 

 

Permanent members have about 10 times as much power!

To calculate the Shapley-Shubik power index of the UN Security Council, we first need the number of sequential coalitions of all 15 members: 15! = 1,307,674,368,000. Now we need to determine the pivotal player in each coalition. Let’s think about how a player could be pivotal: suppose we look from left to right in a sequential coalition and add up the votes. The first time we might encounter a pivotal voter is if the sum is at least 32. This happens if we have so far encountered four permanent and four non-permanent members. So 7 more is needed to the quota, and if the next member in the sequence is permanent, this gives 7 more votes and the quota of 39 is reached. How many ways can this happen? We must choose 4 out of 5 permanent members and 4 out of 10 non-permanent members. These 8 members can be arranged in 8! ways. Next we encounter the last remaining permanent member; there are no choices here. The remaining 6 non-permanent members can be arranged in 6! = 720 ways. So the total number of sequential coalitions for which a permanent member is pivotal following 4 permanent and 4 non-permanent members is

What are the other situations where we might encounter a pivotal voter? Note that we will always have to encounter at least 4 permanent members, since if there are fewer than four, adding one more voter can never bring this number to 5, which is required for a vote to pass. The possibilities are (with the one we already analyzed in the top row):

To tally the number of coalitions in each row, we proceed as in the calculation of the first row that we already did:

• The number of ways to choose permanent members before the pivotal one is 5 choose 4 = 5 or 5 choose 5 = 1 (as in the last row). 
• The number of ways to choose 4 ≤ k ≤ 10 non-permanent members before the pivotal one is 10 choose k. 
• The number of ways to arrange the members so far is (total number of pre-pivotal members)! 
• The number of ways to choose the pivotal member is 1 (there is one remaining permanent member), except in the last row, where it is 7 (there are 7 remaining non-permanent members and we have to choose one).
• There are n remaining non-permanent members remaining, where n could be between 0 and 6, and they can be arranged in n! ways.

The calculations for each row are then:

A permanent member is pivotal in the total of 1,283,288,832,000 coalitions (adding the numbers in all but the last row). Since everything we did is symmetric with respect to the different members, any particular permanent member is pivotal in a fifth of the coalitions, i.e. in 1,283,288,832,000/5 = 256,657,766,400 of them.  A non-permanent member is pivotal in 24,385,536,000 coalitions (last row). Then any particular non-permanent member is pivotal in a tenth of the coalitions, i.e. in 24,385,536,000/10 = 2, 438, 553, 600 of them. Dividing these numbers by the total number of sequential coalitions, we finally get 

Shapley-Shubik index of each permanent member = 256,657,766,400/1,307,674,368,000 = 0.1963 = 19.63%,

Shapley-Shubik index of each non-permanent member = 2,438,553,600/1,307,674,368,000 = 0.001865 = 0.1865%. 

This power index suggests permanent members have about 100 times as much power!

First, let’s take a look at the initial Banzhaf power calculations. When A has 5 votes, B has 4, and C, D, and E each have 1, the winning coalitions and critical voters are: 

Winning Coalition	Critical Voters
{A, B, C, D, E}	A, B
{A, B, C, E}	A, B
{A, B, D, E}	A, B
{A, B, C, D}	A, B
{A, C, D, E}	A, C, D, E
{A, B, C}	A, B
{A, B, D}	A, B
{A, B, E}	A, B
{A, B}	A, B

 

There are 20 instances when a voter is critical, and A is critical 9 times, B 8 times, C, D, and E 1 time each. This gives the power of each voter as:

A = 9/20 = 45%

B = 8/20 = 40%

C = 1/20 = 5%

D = 1/20 = 5%

E = 1/20 = 5%

 

Now consider the new situation where A and B both have 4 votes, and C, D, and E each still have 1. 8 votes are still needed to win. The new winning coalitions and critical voters are:

Winning Coalition	Critical Voters
{A, B, C, D, E}	A, B
{A, B, C, E}	A, B
{A, B, D, E}	A, B
{A, B, C, D}	A, B
{A, B, C}	A, B
{A, B, D}	A, B
{A, B, E}	A, B
{A, B}	A, B

 

There are now 16 times when voters are critical: 8 times for A and B each. C, D, and E are never critical in this instance. Thus, the Banzhaf power index calculates the voters’ power as:

A = 8/16 = 50%

B = 8/16 = 50%

C = 0/16 = 0%

D = 0/16 = 0%

E = 0/16 = 0%

 

This example illustrates a paradox of the Banzhaf Power Index: though A lost a vote, A’s power increased. Additionally, even though votes were only exchanged between A and B, voters C, D, and E lost all power in this computation. 

If you want more information about the Banzhaf power index, review our previous trivia. Stay tuned to learn if the Shapley-Shubik power index has this same problem!

When the European Economic Community was originally created in 1958, the votes were distributed like this: 

• France – 4 votes
• Germany – 4 votes
• Italy – 4 votes
• Belgium – 2 votes
• The Netherlands – 2 votes
• Luxembourg – 1 vote

In previous trivia, we calculated the Banzhaf power of every country and found that Luxembourg had no power (it was a dummy voter). In fact, if we repeat these calculations with the Shapley-Shubik power index, we find that again Luxembourg had no power: there is no ordering of the six countries where Luxembourg causes the coalition to go from losing to winning. In this original structure, 12 out of 17 total votes were required to win, so a winning coalition had to have at least 70.6% of the votes. 

When new members were added to the European Economic Community in 1973, it was decided that England should have the same number of votes as France and Denmark and Ireland should have more votes than Luxembourg but fewer than Belgium and the Netherlands. To accomplish this, the original votes were all scaled by a factor of 2.5, with the exception of Luxembourg’s votes, which were only doubled. Thus the weights were apportioned like this:

• France – 10 votes
• England – 10 votes
• Germany – 10 votes
• Italy – 10 votes
• Belgium – 5 votes
• The Netherlands – 5 votes
• Denmark – 3 votes
• Ireland – 3 votes
• Luxembourg – 2 vote

The number of votes required for passage was similarly scaled to 41 votes, so that it still required 70.7% of the votes to win. 

In this new structure, according to the Shapley-Shubik power index, Luxembourg is no longer powerless! If Luxembourg joins the coalition {France, England, Germany, Italy, Luxembourg} last, they are the pivotal voter. Hence, they have some power. Luxembourg’s power increased despite the fact that its votes were scaled by a smaller factor than every other original member. In fact, even if Luxembourg still had only had 1 vote after the new members were added, they would still be pivotal in this coalition, so their power still would have increased.

Let’s say we have n voters and a weighted voting system where they all have equal weights. The Banzhaf power index is calculated by dividing the number of times a specific voter is critical by the total number of times all voters are critical. Since the denominator deals with the total number of critical voters for the whole voting system, it will stay the same no matter which voter’s power is being calculated. Recall that a voter is critical for a winning coalition if, without them, the coalition does not have enough votes to win. Since all the voters have the same weight, all voters are critical the same number of times. Thus, the numerator will also be the same for every voter. This means that the Banzhaf Power index will give the same power to every voter.

Similarly, the Shapley-Shubik power index is calculated by dividing the number of times a voter is pivotal by n!. Again, the denominator is the same for every voter since n! is a constant that does not depend on coalitions. Recall that a voter is pivotal if, after they join a sequential coalition, it goes from losing to winning. Since the voters all have equal weights, anytime one voter is pivotal, we can replace them with any other voter. Thus, every voter is pivotal the same number of times, and so the numerator is also the same for every voter. Therefore, the Shapley-Shubik power index will also give the same power to every voter.

Notice that with each of these calculations, since every voter gets an equal share of the power and the sum of the power of all voters must be 100%, we know each voter gets 1/n of the power according to both power indices. This means that even though the Banzhaf and Shapley-Shubik indices often give very different calculations of power, this is an instance whey they agree.