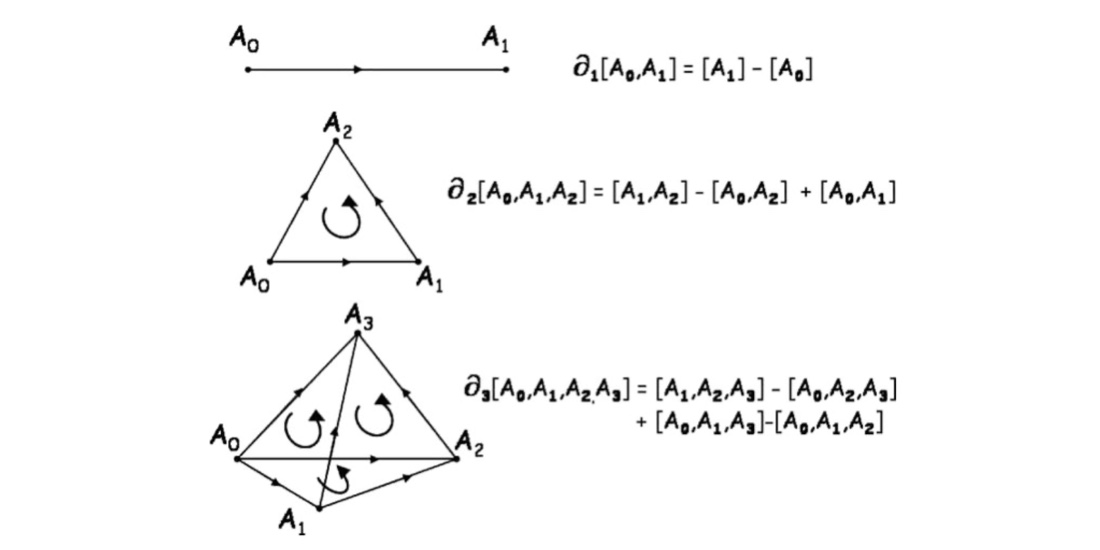
Combinatorial topology and political structures

A recent paper A qualitative theory of conflict resolution and political compromise by Abdou and Keiding provides a model for conflict and compromise in terms of simplicial complexes where vertices are agents and simplices represent coalitions. This structure allows for the modeling of more complicated, or delegated, compromises. The authors also have an interpretation of a homotopy equivalence (or something closely related to it) between two simplicial complexes.

A natural next question, investigated by Andrea Mock of Wellesley College, is what the homology of these complexes might be encoding. Interpreting loops and higher “holes” in the language of game theory is an exciting idea. In addition, it seems that the notion of merging or splitting coalitions can be captured by some kind of a simplicial set, which would bring in the full machinery of simplicial algebraic topology. Finally, since this project is essentially about basic homology theory, it is probably feasible to rework these ideas in an axiomatic, category-theoretic way.