Report: Deficiencies in Recent Research on Ranked Choice Voting Ballot Error Rates

Alan Parry, PhD, Associate Professor of Mathematics, Utah Valley University

John Kidd, PhD, Assistant Professor of Statistics, Utah Valley University

Executive Summary

• This report discusses recent research on ranked choice voting (RCV) and ballot error rates. 
• Several studies indicate that ballot error in RCV elections follows the same patterns as error in non-RCV elections. However, two new studies – More Choices, More Problems? Ranked Choice Voting Errors in New York City and Ballot Marking Errors in Ranked-Choice Voting – claim that RCV increases ballot error rates. We show that both studies suffer from serious methodological and analytical flaws – the former from statistical analysis concerns and lack of suitable control cases, and the latter from false equivalence. 
• Overall, relatively few ballots in RCV elections contain an error, and even fewer ballots are rejected. For most ballots containing an error, the voter’s intent is clear and the ballot is counted as intended. 
• Future research should contextualize the impact of RCV more comprehensively, and compare RCV and single-choice voting more carefully. For example, if RCV and single-choice voting differ in terms of ballot error, that difference should be weighed against the fact that RCV makes more ballots count meaningfully. Recent research shows that RCV causes an average of 17% more votes to directly affect the outcome between top candidates. 

 

Introduction

There is currently much debate on whether ranked choice voting affects ballot error rates, and/or exacerbates ballot error inequality between demographic groups. Two recent papers – Ballot Marking Errors in Ranked-Choice Voting by Stephen Pettigrew and Dylan Radley, and More Choices, More Problems? Ranked Choice Voting Errors in New York City by Lindsey Cormack attempt to address this question, but both have notable limitations. This report analyzes these limitations.

RCV ballots are, by nature, more complicated than single-choice ballots. This is due to the fact that RCV takes more of the voter’s opinion into account when determining a winner. However, a consequence of using a more complex ballot is that it creates more ways that a person could fill one out incorrectly. However, not all “incorrectly filled” ballots in an RCV election are problematic. Most likely indicate a political expression rather than voter confusion. Which types of incorrectly filled ballots are considered problematic plays a role in the validity of the two papers we are analyzing.

Most of RCV’s growth in the United States has happened in the last five years or so, and most political science questions require decades of observations before they can be decisively answered. Both papers primarily consider either the first or second time a municipality used RCV, or only consider a single time or two in a long history of using RCV. One might expect error rates in a municipality to decrease over time as voters become more accustomed to using RCV. This raises concerns about the generalizability of the observations made in the papers.

Studying election methods can be difficult for a variety of reasons, including data availability, sample size, and identifying proper controls for a study. RCV has been implemented in a small number of municipalities. Some of these have distinct characteristics making them different from the general United States population. Comparisons to single-choice elections must be done carefully, and on similar elections, to ensure the results are not confounded by other factors that may be unaccounted for or unmeasured. Both papers discuss differences in the elections utilized for their analyses, raising concern of whether the results are due to differences in single-choice voting and RCV, or due to other factors.

In any statistical study, it is important to use appropriate tools and unbiased interpretations of results. In both papers, there are issues of one or both of these types. Proper statistical interpretation is therefore impossible, and the resulting conclusions are questionable. 

Finally, any drawbacks of a system are relative to the benefit the system produces. If RCV does result in a marginal increase in ballot rejections due to error, this might be balanced by an increase in inclusion of other ballots that might not have impacted the outcome otherwise. For example, RCV greatly reduces the number of voters who lose influence due to voting for a “spoiler” candidate. If that reduction is large in comparison to the increase in rejected ballots due to error, such an increase might be preferable as it results in a net gain in representation.

This report shows how these concerns apply to recent studies by Stephen Pettigrew, Dylan Radley, and Lindsey Cormack, and shows that the conclusions of those reports should be treated with caution.

 

Errors in RCV Elections

Because RCV elections take into account more information about a voter’s opinion, ballots used in RCV races are more complex than those used for single-choice races. This increases the possible ways in which a ballot may be incorrectly filled out. Both the Pettigrew and Radley paper and the Cormack paper discuss potential increases in voter error due to this added complexity.

To be specific, in a single-choice election, ballots typically include a list of candidates with a bubble next to each name. Voters are instructed to fill in a single bubble. The only possible incorrect ways to fill out such a ballot (i.e., an “error”) are (1) leaving the ballot blank, (2) marking bubbles for multiple candidates (over-voting), or (3) incorrectly marking a bubble (e.g., not filling in the bubble entirely). While leaving a ballot blank most likely indicates a desire not to vote in that election, the other two issues are likely true errors on the voter’s part where they accidentally indicated something they did not intend. However, the main reason these ballots are rejected is because it is impossible to glean what a voter’s intention was from them.

On the other hand, ballots in RCV elections typically look like the ballot in Figure 1. Each column indicates a position in a rank order, while each row indicates a candidate. Voters are instructed to rank the candidates in order of preference, indicating which candidate is in which position by filling in the bubble that is in the row of that candidate and column of that position. A correctly filled out ballot would have exactly one bubble filled in each row and each column. An example of a correctly filled out ballot is on the right side in Figure 1.

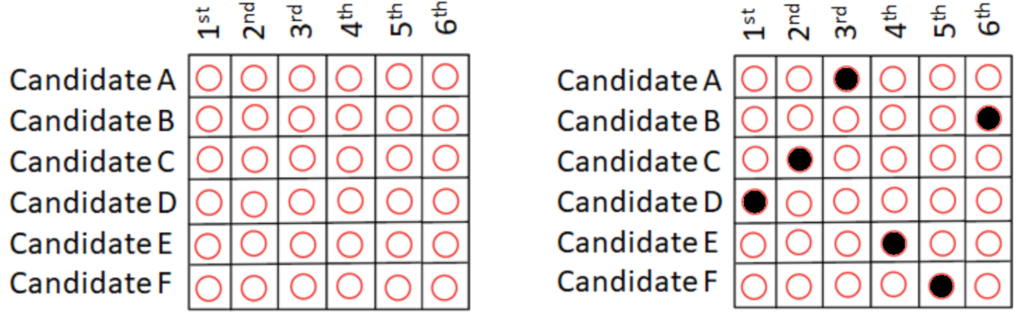
Figure 1. A blank RCV ballot and an example of a correctly filled RCV ballot.

Because the task of filling out an RCV ballot is more complex than the task of filling out a single bubble, there are a few additional ways to incorrectly fill one out. The three types of incorrect ways to fill out an RCV ballot (i.e, an “error”) that each paper considers are 

1. over-ranking a candidate,
2. skipping rankings, and 
3. over-voting a ranking. 

Examples of these errors are in Figure 2.

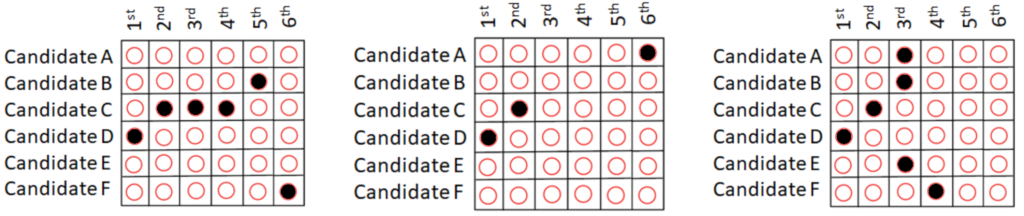
Figure 2. Types of errors in an RCV ballot. From left to right these errors are (1) over-ranking a candidate, (2) skipping rankings, and (3) over-voting a ranking.

Over-ranking a candidate occurs when a voter lists the same candidate for multiple rankings. That is, a single row has filled bubbles in multiple columns.

Skipping rankings occurs when a voter does not indicate a preference in one or more columns between columns in which they do indicate a preference. That is, when a voter does not rank all the available candidates, and ranks one or more candidates several rankings below another candidate with no preferences in between. Skipping rankings at the bottom is not considered a skipping error.

Finally, over-voting a ranking occurs when a voter lists more than one candidate in a single ranking position. That is, a single column has filled bubbles in multiple rows. This is essentially the same type of error made on a single-choice ballot when a voter marks multiple candidates for a single race. The error on an RCV ballot corresponding to this type of error in a single-choice ballot would be marking multiple candidates in the first-choice column. However, since there are multiple columns in an RCV ballot, the number of possible ways to make this type of error are higher in an RCV election than in a single-choice election.

Errors only matter if they result in a rejected ballot. Ballots are usually rejected when there is nothing left on them that can be correctly interpreted. For example, suppose one has an RCV ballot that correctly indicates a first and second choice preference, but then over-votes the third choice column by marking two or more candidates in that column (see Figure 3 for this example). This ballot would count as intended for the voter’s first and second choices, because until the third choice column, the voter’s preference can be correctly understood. Only at the over-voted column does the ballot become impossible to interpret. As such, only when the voter’s first and second choices are eliminated would the remainder of the ballot be rejected.

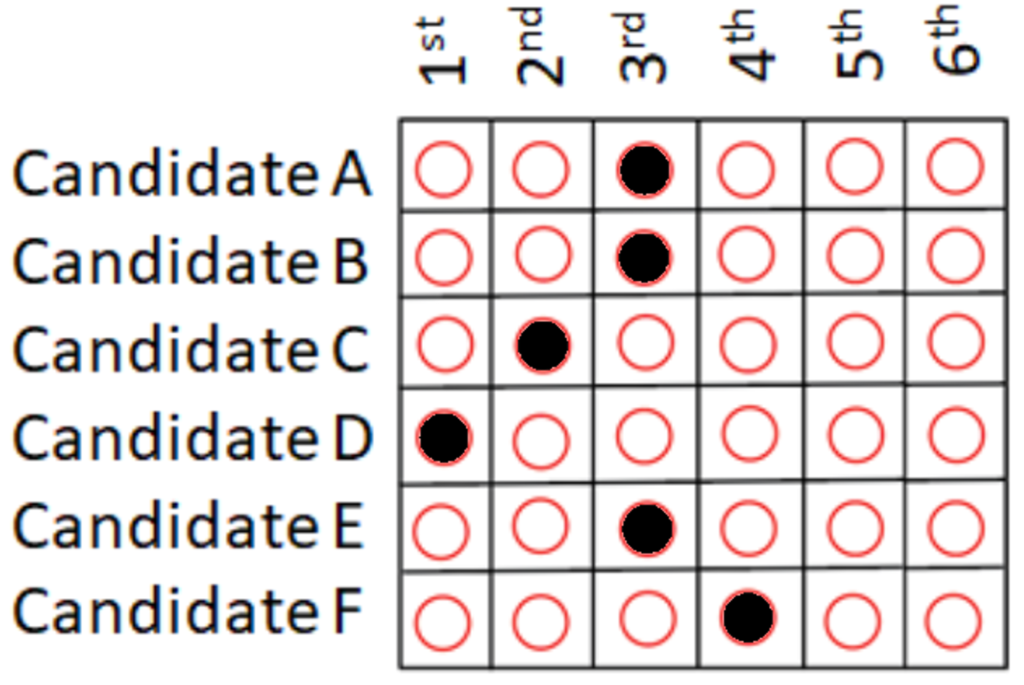
Figure 3. Over-vote error in which the voter’s first and second choices count as intended. But if those candidates are eliminated, then the remainder of this ballot would be rejected because it is unprocessable from that point on.

The first two types of errors listed for an RCV ballot – over-ranking and skipping rankings – are not particularly problematic. In fact, the vast majority of ballots with an over-ranking or skipping error are counted, and only a few municipalities have rules for rejecting them. There is no mathematical reason why these ballots should ever be rejected, as every one of them can be processed correctly by the instant run-off procedure with no issues.

There is no mathematical reason to reject a ballot with a skipped ranking because skipped rankings can be correctly processed by the instant run-off procedure. Indeed, skips occur naturally on ballots while being processed by the procedure. For example, consider a correctly filled RCV ballot in an election with four or more candidates using instant-runoff voting. If the voter’s first choice is not eliminated in the first round, then a different candidate is eliminated. This elimination results in a skip in this voter’s ballot in the column where they ranked the eliminated candidate. But the instant-runoff procedure has no problem tallying that vote, even if in a later round, that voter’s first choice candidate is eliminated. Whenever a skipped or eliminated ranking is encountered, the procedure simply continues going down the list until it finds a ranking that is not skipped.

Ballots with skipped rankings can be correctly processed in the same way. For example, an RCV ballot that ranks candidate B first, D second, and A fifth, while skipping rankings three and four, is treated as though the voter ranked B first, D second, and A third. Thus, there is no issue with how to interpret the ballot. That said, it is impossible to determine the voter’s intention with this ballot. On one hand, A could be the voter’s third choice, but they just like A far less than B and D. On the other hand the voter could mean that they cannot decide between unranked candidates C and E, but that A is their last choice. If the prior is the case, then the instant-runoff procedure interprets the ballot as the voter intended. If the latter is the case, then the procedure interprets the ballot slightly differently than the voter intended since it makes their “last” choice simply their third choice. However, we should not be in the business of second guessing voter intent. In either case, since the ballot is readable in the procedure, the ballot should be processed as the voter filled it out.

Similarly, there is no mathematical reason to reject an over-ranked ballot where one candidate is listed for multiple rankings. This is because when the instant-runoff procedure considers the ballot, if it encounters an over-ranked candidate, it will treat that candidate as being ranked in the highest position listed. If that candidate is eliminated, then they are eliminated from all positions. The ballot will now simply have “skips” wherever that eliminated candidate was ranked and we already explained how the instant-runoff procedure addresses skips.

Thus, there is no mathematical reason to reject an RCV ballot that includes an over-ranking or skipped ranking. (We also note that there is no advantage, mathematical or otherwise, to over-ranking a candidate or skipping a ranking.)

Pettigrew and Radley make curious arguments about the validity of ballots that have a skip or over-ranking. They claim that skipping candidates usually only occurs if a voter does not understand how the instant-runoff procedure works or what the jurisdiction’s rules are about ignoring skips. In fact, they claim that the number of people who skip rankings and understand the instant-runoff procedure is small, and hence all skips should be treated as errors. However, at the same time, they argue that over-ranking a candidate is usually a form of political expression and is not due to a voter misunderstanding how the instant-runoff procedure works.

Since neither skips nor over-rankings carry any advantage in RCV elections, how can one argue that one is based on misunderstanding the process, but the other is a form of political expression? Voters who use skips or over-rankings are not doing anything that would provide them an advantage, so their understanding of the instant-runoff process and what strategies are effective is arguably about the same. 

Just because someone employs a poor strategy does not imply that it was unintentional nor that it should be counted as an error. For example, voting for a third-party candidate in a two-party dominated plurality election is also a poor strategy, since it means that the vote will not count in the final tally that determines the winner. Does that mean people who vote third party misunderstand how votes are counted in a plurality election, and hence all votes for third party candidates should be considered errors? Of course not! It is clearly possible that voting for a third party is a form of political expression. In the same way, skipping or over-ranking candidates could be a form of political expression too.

Bad strategies abound with any voting method. The effectiveness of someone’s strategy or political expression is not relevant. The fact remains that in the case of a ballot with skipped positions or over-rankings, the voter chose to rank some candidates in an order they determined, and the ballot is processable. Thus, we should process it as is; we should not second guess a voter’s intention, political expression, or education about a voting method.

Poor strategies lead to unfavorable outcomes all the time. That does not mean the people using poor strategies accidentally filled their ballot out incorrectly. There is a big difference between making an unintentional error and making a deliberate choice for which one does not fully understand the consequences. Deliberate choices are no more errors than voting third party in a plurality election.

In fact, some unintentional ballot errors may even be undetectable. For example, a voter might accidentally mark the bubble for a candidate they did not intend, not notice the error, and submit the ballot with their unintended vote. But there is no way for a county clerk to detect that error short of verifying every vote with the voter. In which case, what is the point of the ballot in the first place?

The only objective way to determine whether something is a meaningful error is whether it makes the ballot unprocessable. Of the types of errors discussed in both papers, only over-voting a ranking does this.

Indeed, the findings of these papers appear to support the idea that over-voting is the most impactful type of error. For example, in the Pettigrew and Radley paper, they indicate that 4.8% of ballots in the RCV elections considered contained an error of some kind, and the breakdown of errors was that 2.0% made a skipping error, 2.4% made an over-ranking error, while only 0.6% made an over-voting error (see Figure 5 of that paper). The fact that those sum to 5.0% instead of 4.8% means that 0.2% of ballots made more than one error. 

Of the ballots that contained a skipping error, only 5.8% were rejected. Of those that contained an over-ranking error, only 1.5% were rejected. Of those that contained an over-voting error, 65.8% were rejected (see Figure 10 of that paper).

While rates of skipping rankings and over-ranking are higher than rates of over-voting, the rejection rates for these errors are very low, suggesting that most jurisdictions have identified that skipping and over-ranking do not result in unprocessable ballots. The rejection rate for over-voting is much higher because at least some of the ballot is unprocessable. However, not all these ballots are rejected because frequently at least part of the ballot is processable (see Figure 3 for an example). In that case, rankings are counted as intended until it can no longer be gleaned how to process the ballot.

In fact, Pettigrew and Radley investigate the number of ballots that have multiple types of errors. This analysis yields an interesting observation. Of the ballots that skipped a ranking, about 5.8% of the ballots were rejected (see their Figure 10), while 7.8% of ballots that skipped a ranking also contained an over-voted ranking (see their Figure 15). Similarly, of the ballots that over-ranked a candidate, only 1.5% of the ballots were rejected (see their Figure 10), while 1.6% also over-voted a ranking. Since the number of rejected ballots in each case is less than the number of ballots that over-voted a ranking, it is possible that the ballots were rejected not because of the skips or over-rankings, but because of the over-vote errors. That is, the above data is consistent with the hypothesis that no ballot was rejected because of a skip or over-ranking error, and ballots were only rejected because of over-voting errors. 

	Rejected	Contained an over-vote
Skipped a ranking	5.8%	7.8%
Over-ranked a candidate	1.5%	1.6%

Table 1. Percentage within rows

Given that some jurisdictions in the study have rules for rejecting ballots based on a skip or over-ranking error, this hypothesis is probably not true, and some ballots were likely rejected that did not contain an over-vote. 

In the elections considered, about 0.6% of ballots contained an over-voting error, of which 65.8% were rejected. This means that about 0.39% of total votes were rejected because of an over-voting error. The total percentage of ballots with an error was 4.8%,of which only about 9.8% were rejected. This means that 0.47% of ballots were rejected because of any kind of error. This means that of ballots that were rejected because of any kind of error, about 84% contained an over-voted ranking. Thus while the hypothesis that no ballot was rejected without an over-vote seems to be false, it does appear safe to say that the vast majority of rejected ballots were rejected because of an over-voted ranking. This supports the notion that the error that mattered most was over-voting, because that’s the only error that makes a ballot unprocessable.

 

General Criticisms of Both Papers

It is expected that there will be an increase in errors for any new procedure that is implemented in any field. If all new advancements were discontinued due to this initial trend, many items and practices that are commonplace today would have been discontinued early in their development (see, for example, most medical procedures, especially cardiac surgeries). Similarly, with RCV, an initial increase in ballot marking errors when compared to single-choice ballots is likely inevitable. 

A more comprehensive view of errors would consider changes in error rates over time. Both the Pettigrew and Radley paper and the Cormack paper focus only on one or two consecutive voting periods in each RCV jurisdiction, and most were the first or second time the jurisdiction had used RCV. Thus, any comparison to single-choice ballots provides a biased representation favoring the method that has been used for a longer period of time and is more familiar to voters.

Furthermore, causation is incredibly difficult to prove. A primary method to show causation is to remove all confounding effects by making the two groups being compared as similar as possible. In comparing elections with very different stakes and publicity, or comparing elections held in two very different voter populations, these papers risk misattributing the error rates to RCV when they might be due to other factors. Thus, claims that differing error rates were caused by voting methods cannot be decisively shown.

For example, the Pettigrew and Radley paper compares the first two times that RCV was used in Alaska with a few RCV elections in San Francisco – a municipality that has used RCV for more than decade. Because the error rates in Alaska were lower than in San Francisco, they claim that this shows that error rates do not necessarily decrease over time as a municipality gets used to using a voting method. However, there are many differences between San Francisco and Alaska, and the disparity in error rates between the two may be due to these differences. Thus, to make the claim that is made, one would need to control for these differences, or they would need to compare the ballot error rates of an early use of RCV and a later use of RCV in the same municipality for a similar type of election. This latter approach would be the only way to start making the claim about error rates over time. The fact that this paper does not consider this significant confounder to their finding is troubling.

 

Specific Issues in the Cormack Paper

According to studies from 2016 and 2021, RCV elections have comparable ballot error rates to those in non-RCV elections. A 2020 study reveals no significant differences in error rates when comparing racial and ethnic groups. Cormack’s primary hypothesis is that there is an increase in error rates using RCV when compared to single-choice ballots.  She also proposes several secondary hypotheses that similar differences would be found within various demographics. She finds no significant difference in the overall error rates between the two methods and hence fails to support her primary hypothesis. However, she continues conducting analyses of her secondary hypotheses and reports potential differences between RCV and plurality among various subgroup demographic analyses. This is contrary to best statistical practices where secondary hypotheses should only be considered when the evidence supports the primary hypothesis. Otherwise, spurious findings are likely to occur by chance. 

Additionally, Cormack claims that demographic disparities in error rates are more pronounced under RCV than in single-choice elections. Cormack uses a sample size of three elections – one RCV and two non-RCV. But both non-RCV elections were less meaningfully contested, even though they were intended as control cases. The RCV election in her study included over a dozen candidates, while the two control elections were both from deep-blue New York City, featuring popular incumbents who each sailed to victory with over 70% of the vote. Intuitively, one would expect ballot error rates to be affected by the size of the candidate field and competitiveness of the race, but Cormack does not appear to consider this potential source of differences in error rates. Without a proper control election, any difference in error rates cannot be meaningfully separated from the difference caused by election competitiveness. Thus, Cormack’s comparison of a competitive RCV election to less competitive control elections might produce unreliable results.

Cormack also utilizes linear regression for her analyses. While an oft-used tool and highly effective in correct scenarios, linear regression is only appropriate when conducting analyses for relationships that are linear. One example of this in Cormack’s work considers the share of the population with a Bachelor’s degree. While the error rates are elevated for communities with a low prevalence of Bachelor’s degrees, the error rates quickly level off as the prevalence increases, making the data clearly nonlinear. However, Cormack models it with linear regression anyway.  This type of data pattern, as well as other patterns seen in various graphs within the paper, may be indicative of other violations of linear regression assumptions, causing any results to be questionable. 

 

Specific Issues to the Pettigrew and Radley Paper

There is much in the paper by Pettigrew and Radley to cause concern regarding bias. Many plots are presented in a way that confuses the size of error rates in RCV elections. For example, the y-axes of the four graphs of Figure 9 are each different, making these plots difficult to compare at a glance, which could be misleading. Moreover, important statistical processes are not described, and others such as multiple-corrections appear to have been neglected. 

Lastly, wording throughout emphasizes the shortcomings of RCV elections, while glossing over the limitations of non-RCV elections. One particularly egregious example is that Pettigrew and Radley claim RCV votes are 10 times more likely to be rejected due to error compared to votes in non-RCV races, and that overvote errors are 14 times more likely to occur in RCV elections compared to non-RCV ones.  While these differences sound sensationally large when phrased like this, the actual error rates provide a much clearer picture of what is happening.  The overall average rejection rate found in this paper for RCV elections was 0.53% compared to 0.04% for non-RCV elections.  Moreover, the average overvote rate for RCV elections was 0.60% while for non-RCV elections, it was 0.04%.  While these error rates are indeed about 10 times and 14 times larger (respectively), 14 times a small number is still a small number.  Using sensationalized language of this type to exaggerate the impact of this difference indicates significant bias in the presentation of these results.

Even if the above criticisms of increased error seen under RCV are true, these concerns still fail to account for the other benefits that can be gained through RCV. Using RCV, more voters are able to participate in the choice of the final winner, and voters also have more freedom of political expression. In fact, research shows that when using RCV, on average 17% more votes directly affect the outcome between the final two candidates. This is due to the fact that voters select backup choices in case their top choice is eliminated.

A fair comparison between RCV and single-vote elections would compare the mild increase in ballot rejection caused by errors to the massive increase in ballots that impacted the outcome, especially if the claim being implied is that “RCV makes fewer votes count.” In this case, the average 17% increase in meaningful votes using RCV is considerably larger than the average ballot rejection rate of 0.53% using RCV observed by Pettigrew and Radley (and with tongue firmly planted in cheek, we point out that this is, in fact, about 32 times larger). Also worth considering is a recent statistic – in all RCV elections in the U.S. with 3 or more candidates (for which we have a cast vote record), the median first-round overvote rate is 0.15%.Thus, even with the increase in error rates, there is an overall net gain in voters impacting the outcome of the election.

 

Conclusion

We appreciate our colleagues’ attempts to answer important questions about voter behavior, and the challenges that come with investigating a relatively novel topic in the U.S. However, that does not preclude the importance of proper scientific analysis and discussion. It will take more election cycles and observations, and more precise statistical analyses, before we can definitively say whether RCV impacts ballot error rate patterns, and whether those differences are outweighed by other impacts of RCV.