With the old profile:

A won. Then 5 voters who previously preferred B to A changed their preference and now rank A higher than B, so the new profile looks like:
Now B has the fewest first place votes, so the runoff gives:

C wins the election 14-13!
Rankings that were switched had nothing to do with C since voters only changed their preference for A and B, yet this made C win! A actually did better in the election when fewer people liked her. This is called the paradox of positive association, or failure of monotonicity. A voting method satisfies the monotonicity criterion if, any time a candidate A is winning an election and a voter changes their preference to move A higher up on their ballot, A should still win. Our example shows that runoff voting fails the monotonicity criterion.
This example also shows that the runoff method is susceptibil to strategic or insincere voting. In this example, supporters of C could have ranked A and B strategically (not according to their actual preference of A versus B) to move C higher in the rankings.
As this example demonstrates, calculating a group’s preference is not always straightforward. We expect individuals to have preferences and to act according to them. Individual’s actions are assumed to be rational and predictable, but group preferences do not behave like this. Instances like the paradox of positive association show groups do not have preferences nor can we expect them to act as if they had them. Studying the behavior of groups and their opinions is the field of social choice theory.
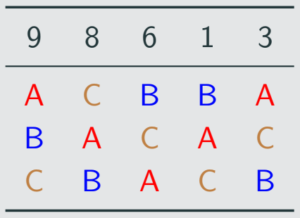
After candidate C drops out, the Borda count on the new profile is:

After Oklahoma and the extra seats were included in the calculation, the fractional parts of the population/s for each state decreased. Since New York’s population/s was greater than Maine’s, its fraction decreased more, enough to give Maine the extra seat.
While the Alabama paradox was avoided by permanently setting the number of representatives, and the population paradox was only found through experimenting with calculations, the new states paradox was a problem that could not be controlled by Congress. In 1911, soon after the discovery of the new states paradox, Hamilton’s method was abandoned.
points for A : 3 · 1 + 2 · 2 + 2 · 0 = 7
points for B : 3 · 0 + 2 · 1 + 2 · 2 = 6
points for D : 3 · 2 + 2 · 0 + 2 · 1 = 8
Now D wins! Since the relationship between candidates A, B, and D changed after another candidate was removed, this example shows that Borda count is not independent on irrelevant alternatives.
Failure of IIA has affected real world elections. In the 1995 Figure Skating World Championship, before American skater Michelle Kwan skated, the leaderboard looked like:
- First place: Chen Lu (China)
- Second place: Nicole Bobek (USA)
- Third place: Surya Bonaly (France)
Then, after she skated, it looked like:
- First place: Chen Lu (China)
- Second place: Surya Bonaly (France)
- Third place: Nicole Bobek (USA)
- Fourth place: Michelle Kwan (USA)
Even though Kwan came in fourth, Bobek and Bonaly switched places. This is a failure of IIA because a candidate’s place should not be affected by the placement of candidates below them. The skating community has since changed their scoring methods in an attempt to avoid this problem.
Of the voting methods we’ve explored so far, plurality, Borda count, Instant runoff, and Condorcet method all fail IIA. This does not mean every election using these methods will exhibit the failure of IIA, just that it might.
All of the above methods satisfy another condition called the Pareto criterion. We will explore this criterion and its connection to the IIA in future posts.
The idea of the Pareto criterion comes from economics, where one outcome is “Pareto optimal” if no possible alternative is preferable. A candidate can also be Pareto optimal if no other candidate is preferred by every voter. If a voting criterion satisfies the Pareto criterion, every winner must be Pareto optimal.
Luckily, since the Pareto criterion is desirable for an ideal voting method, most of the methods we’ve seen so far satisfy this condition:
- Plurality satisfies Pareto:
- Plurality counts the number of first-place votes a candidate receives. If everyone ranks A over B, B cannot receive any first-place votes, so B cannot win.
- Dictatorship satisfies Pareto:
- If all voters rank A above B, this includes the dictator. Since the dictator ultimately decides the winner, B cannot win.
- Monarchy does not satisfy Pareto
- In a monarchy, one candidate wins no matter how other voters feel. Therefore, even if everyone prefers A over B, B could still win if they are a monarch.
- Borda count satisfies Pareto
- If B is always ranked below A, then A will receive at least one more point on every ballot than B. Therefore, B can never get more points than A, so B cannot win.
- Instant Runoff satisfies Pareto
- If every voter prefers A to B, then B gets no first-place votes. This means either there’s a majority winner that is not B or B gets eliminated before A.
- Condorcet method satisfies Pareto
- If every voter likes A more than B, A will win the pairwise contest between A and B, so B cannot win.
One interesting observation is that Plurality, Borda count, Condorcet method, and instant runoff voting, methods that satisfies the Pareto criterion, do not satisfy the independence of irrelevant alternatives. Stay tuned for a future trivia post about Arrow’s Impossibility Theorem, where the connection between these two criteria will be explored.
To understand what’s behind Arrow’s Theorem, it’s helpful to have the Decisiveness Lemma: a voting system in an election with at least three candidates that satisfies both Pareto and IIA will never produce a tie. This is helpful, because this means when we’re proving Arrow’s Theorem, we can assume there is a winner. To prove Arrow’s Impossibility Theorem, let’s assume we have a social choice function with at least three candidates that satisfies the Pareto and IIA conditions.
We first want to show that for every pair of candidates, there exists one voter who can control their outcome. If there are three candidates, A, B, and C for example, we can start by thinking about a profile in which every voter ranks the candidates 1.C 2.A 3.B. By Pareto, C wins. Now suppose voters individually lower candidate C to the third position. We know by Pareto that B cannot win and, once this process is complete, A will win. This also means there is a critical moment where after some voter v switches C to the third position, A becomes the winner.
Now, we can show that if this critical voter places A over B, B loses. Here we can use the Extremal Lemma: if we have a voting system that satisfies Pareto and IIA, like the one in the proof of Arrow’s Theorem, and there is one candidate C such that every voter places C at the top or at the bottom of their rankings, then either C is the winner, or the electorate prefers every other candidate to C. If we assume some of the voters rank C first, others voters rank C last, and only critical voter v ranks A first, the combination of the Extremal Lemma and the IIA and Pareto properties mean A has to win. This means that in any profile there exists a voter v with dictatorial power for A over B.
Now, our goal is to show voter v is a unique voter whose first choice always wins in this social choice function. By rearranging the candidates A, B, and C we can use the same logic to show that for every pair of candidates there exists a dictatorial voter for one candidate over the other. We can also show that this voter must be the same for each pair, otherwise a tie could occur. Therefore, there exists a unique voter with dictatorial power over every candidate. This voter is a dictator and this social choice function must be a dictatorship.
Arrow’s Theorem does not simply say that we have yet to find a social choice function that will satisfy Pareto and IIA; it shows that no such method will ever exist. Arrow’s Impossibility might seem to suggest that a dictatorship is the best voting system. However, we know that dictatorships are inherently unfair. Instead, we can interpret this theorem as saying that no ranked voting system is perfect.
It is important to note that though Arrow’s Impossibility Theorem does say that every ranked-choice voting method besides dictatorship will fail Pareto and/or IIA, it does not say how badly a particular voting system fails at being fair. Arrow himself once said “Most systems are not going to work badly all of the time. All I proved is that all can work badly at times.” This means we can either choose to ignore criteria that we deem least important, or we can analyze various systems and try to choose the one that’s “most fair”, or is least likely to fail various desirable conditions. But this means we have to agree on what the most important conditions are! This is not easy, and there is a vibrant debate about which system should be used and how much of their failure we are willing to live with. Arrow Impossibility only applies to ranked voting systems, so we might consider some non-ranked methods instead.
Let’s consider the perspective of Prisoner 1. They can’t communicate with their co-conspirator, so they have to think through all the possible scenarios given of what Prisoner 2 could choose. If Prisoner 2 decides to stay silent, Prisoner 1 could either get 5 years by also staying silent or zero years by testifying. In this situation Prisoner 1 would certainly prefer no prison time, so they would want to testify. If instead Prisoner 2 testified, Prisoner 1 could get 15 years by staying silent or 10 years by testifying. Again, Prisoner 1 gets a better outcome by testifying. Therefore, Prisoner 1 doesn’t need to communicate with Prisoner 2 to know they should testify! Since the police offered the same deal to both Prisoners, the same logic shows that Prisoner 2 should also testify. Therefore, the outcome of this interaction is that both Prisoners testify and each get 10 years behind bars. Notice that though this is the outcome reached when both Prisoners do what’s right for themselves, the outcome reached when both of them stay silent is actually better for both of them! This is a paradox in game theory known as the Prisoner’s Dilemma that is often observed in politics.
For example, consider the arms race between the United States and Soviet Union in the 1960’s through 1980’s is often considered a Prisoners’ Dilemma. We can think of both countries as having the choice to “cooperate” and decrease their arsenal of nuclear weapons or “defect” and continue increasing their supply. With the threat of mutually assured destruction, both countries likely would have prefered if both of them decreased their supply, thus making it more safe for everyone involved. However, if we think about this from the United States’ perspective, if the USSR chose to disarm, then the United States would have preferred to continue increasing their supply, thus becoming the more powerful of the two countries. If the USSR chose to continue creating weapons, then the US would also have liked to follow suit to prevent the USSR from winning their power struggle. The same logic follows for the USSR. Thus, even though both countries preferred a reality without the constant threat of nuclear war, the arms race continued for several decades.
The Prisoners’ Dilemma appears in many other aspects of life, including in bargaining scenarios like purchasing a car or negotiating a salary, political negotiations such as budget spending and legislation and other international politics like trade wars. This dilemma is closely related to the idea of the “Tragedy of the Commons,” which we will explore in future trivia.
Similar to the analysis of the Prisoners’ Dilemma, we can look at this situation from the perspective of each country. Let’s start with Country A: if Country B chooses to reduce their emissions, then A can increase their revenue by continuing to produce emissions and take over B’s economic loss. Thus, in this case they want to keep producing emissions. If instead Country B continues emitting at their regular rate, Country A can choose between loosing economic power by cutting emissions or remaining competitive by continuing to pollute. Since continuing to pollute is the best outcome for A no matter what B chooses, this is Country A’s dominant strategy. The same logic shows that this is also true for Country B. Therefore, the most likely outcome is that both countries continue to pollute. Notice that there is actually a better outcome for both countries if they both choose to cut emissions! This means that we simply have an incarnation of the Prisoners’ Dilemma.
By considering the cost to the society at large, we see that this is also a tragedy of the commons: if only one out of millions of firms pollutes, we would still have enough clean air to go around. However, when all the firms play this game and choose to continue to pollute, we deplete communal resources and experience negative effects like climate change. Not only did this game produce a less than optimal outcome for the individual countries but also a bad outcome for the global community.
Tragedy of the commons occurs in many places. Any strain on natural resources is an example, such as overfishing, deforestation, or water pollution. One company fishing more than the ecosystem can handle, cutting down an excess of trees, or putting trash in a river is unlikely to cause any of these systems to collapse. However, when all firms see these actions as their individually dominant strategy, we strain our available resources. Purchasing fast fashion, pumping groundwater, and sitting in traffic jams are all other instances of tragedy of the commons.
Tragedy of the commons demonstrates that individuals acting in their own best interest doesn’t always produce an outcome that’s in the best interest of us all. So how can we prevent this from happening? One solution is the use of incentives to encourage individuals to make choices that are better for the community. For example, some cities have passed laws requiring customers to pay for plastic bags at grocery stores. Though the convenience of single use plastic usually means more of these bags end up in the landfill, these laws are incentivizing consumers to think about environmental costs. Now it is individually more expensive to choose the convenient option, so for many shoppers it is now individually optimal to bring a reusable bag. Another solution is direct regulation. When governments set strict limits on the amount of pollutants that can go into the air, companies can no longer treat the environment as an infinite resource.








